|
|
Hi大家好,现在我们来探究一下编程中的递归问题。
首先,内存中被划分了几个区域,分为:
1.堆栈
2.自由存储区
………………………………
其中堆栈是用来专门存放函数的东东们的。
我们来了解一下函数的内存占用(耗费),这是了解递归为什么会有很大耗费的前提:
1.返回类型(魔兽中函数返回类型为nothing时没有内存占用)
2.所有的参数的耗费之和
3.当前处理的语句耗费(视情况而定)
4.所有局部变量的耗费之和
5.命令指针(指向下一个命令)
函数的关于内存的清空及申请:
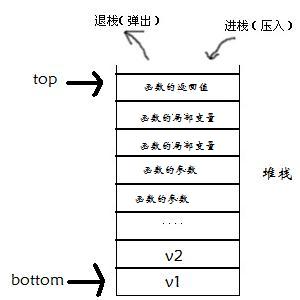
1.函数被调用时,*堆栈将一段空间用来:
存放 一个返回类型的需占用的bit
存放 所有的参数的值(并传递值)
存放 所有的局部变量的值(并初始化)
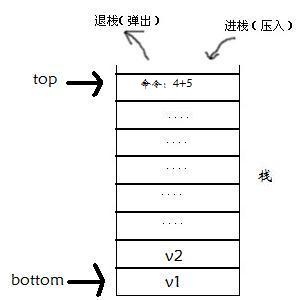
2.函数在运行时,
堆栈会动态地为此函数应运行的一个*命令分配空间。
此命令执行完毕,并清空这个命令的使用的空间,再执行下一命令。
如果是调用其他的函数,所有的空间都不清空,直到这个调用的函数执行完毕。
命令(这名是我瞎编的,理解就好):
如:I = 4 + 5的一行语句。
它有2个命令:
1. I=(赋值)
2. 4+5(运算)
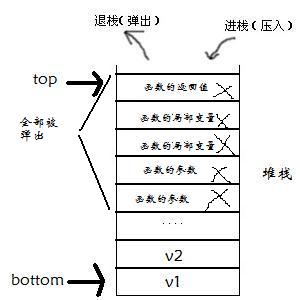
3.函数执行完毕/返回一个值(最后的语句也执行完了),清空:
局部变量:
1.基本类(integer、real等)的空间
2.Handle类被设置成null的空间
参数:
所有的参数不分类型全被清空
返回类型:
在将返回类型传递给调用自己的函数后,清空。
函数运行时,函数使用的这些空间被标记;此函数[结束]时,电脑(应该是CPU)按照标记来清空此函数使用的内存。
然后,我们来了解一下[堆栈]:
堆栈是用来存放电脑程序执行等的地方。
所有的函数的申请的内存全在这里。
堆栈是一个栈,而栈是:
栈(stack)可定义为元素在表的末端进行插入和删除的线性表。
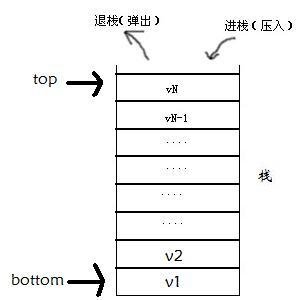
允许插入和删除的一端为栈顶(top)
(如果元素插入,top指向新的元素/如果元素删除,top指向它的下面的元素,无元素时top一般指向-1)
相反的,不允许插入和删除的一端为栈底(bottom)
(通常top和bottom指的是那一端上的元素)
设栈S=( vN, vN-1, ..., v2, v1 )
(v为栈中的元素)
则所有元素压入栈的顺序为:
v1, v2, ... , vN-1, vN
弹出的顺序为:
vN, vN-1, ... , v2, v1
与压入的顺序正好相反。
分析一个元素vN的入/出顺序,可得:
栈中元素后进先出
分析另一个元素v1的入/出顺序,可得:
栈中元素先进后出
这两句话说的都是一个意思,理解就好。
接下来,我们看一下函数运行中在堆栈中的动作:
被调用时:
运行时:
执行完毕时:
而一个递归函数(而魔兽的递归函数,只能由自己调用自己。)是怎样运行的呢?
1.运行时,调用自身
2.被调用者初始化(比如获得参数什么的)
3.不断循环1、2步骤,直到最后一个被调用者停止递归(并返回),堆栈清空这个被调用者的内存,返回至调用者,继续执行,执行完毕(并清空)后,再返回至这个调用者的调用者………………如此循环反复,直到第一个被调用的递归函数执行完毕,递归停止。
我们来看一个递归的图:
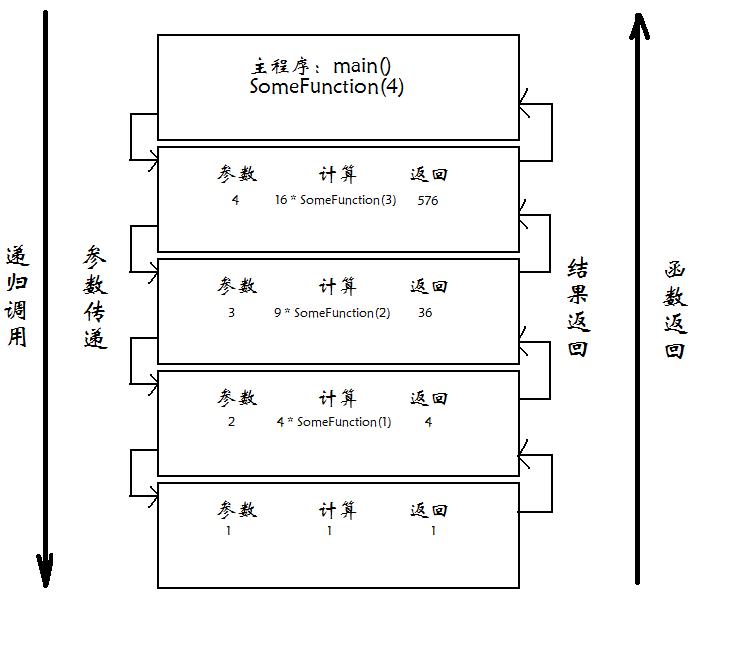
请大家注意:
在递归的前进(函数执行完毕/返回之前)的过程中,堆栈是不会被清空的,直到函数执行完毕。
也就是说,如果递归5次,
则有:堆栈中这个函数最多的内存占用情况(此时没有任意一个递归函数执行完毕/返回,只是每个函数都执行到调用自己的那个命令,并等待下一个自身的返回,而最后的那个自身,则满足了递归出口的条件,遇到了递归出口,但还没返回)为:(5+1)*每一次函数的耗费
而Jass是一门高度整合的编译语言,递归会有比C++,Java等语言高几倍的耗费。
所以说要尽量避免使用递归。
递归中最重要的是设置递归的出口和递归出口的条件,也就是在什么情况下,函数不再向下递归。
如果不设置出口,则函数会永久的调用下去,直到堆栈再也没有空间可以分配,后果就是游戏结束(这还是魔兽的结果,要是换成C++、Java,估计电脑就没法用了)
下面是SomeFunction的代码:
[codes=jass]function SomeFunction takes integer i returns integer
if i <= 1 then //递归出口的条件
return 1 //递归出口
endif
return i * i * SomeFunction(i-1) //递归
endfunction[/codes]
基于尽量避免使用递归,那应怎样改进算法,让算法花更少的耗费呢?
现在我给出一小部分的递归的替代方法——
迭代
迭代可以有效地替代【单向/尾】递归。
迭代的最高耗费:运行一次函数的耗费。
递归的最高耗费:递归的次数 * 运行一次函数的耗费
那什么是迭代呢?
迭代就是将有穷个变量作为参数,根据参数作不断的循环运算(有穷次)出结果后又将结果赋给用作参数的变量。
而循环运算终止的条件就是递归出口的条件。
比如著名的斐波那契数的递归算法是:
[codes=jass]function Fib takes integer i returns integer
if i <= 2 then
return 1
endif
return Fib( i - 1 ) + Fib( i - 2 )
endfunction[/codes]
而它的非递归算法为:
[codes=jass]function Fib takes integer i returns integer
local integer j = 2
local integer first = 1
local integer second = 1
local integer Current = 1
loop
exitwhen j >= i
set j = j + 1
set Current = first + second
set first = second
set second = Current
endloop
return Current
endfunction[/codes]
而比较复杂的【单向/尾】递归,就可以看看我在《【环保大师】教你“环保”(排泄+提高效率+一点小建议)》一帖中提高效率的(1)严禁:递归,应该对你有帮助。
PS:计算斐波那契数列的最高效算法是利用递推公式得到的公式直接求解。
Fib(n) = 1/sqrt(5) * [ ((1+sqrt(5))/2)^n - ((1-sqrt(5))/2)^n ]
//sqrt = SquareRoot
至于怎么推的,自己去查吧^_^
最后,我们来分析一下著名的雪花函数(至今你还能在Jass区->算法区找到这个帖子)
请先观看这个帖子…………
…………
…………
观看完这个帖子,我们可以把这个雪花函数抽象成4叉的递归问题。
一个雪花函数会顺序地调用4次自己,每次坐标都不同。
[codes=jass]function Snow takes real x, real y, integer i returns integer
if ( i == 0 ) then
return
endif
//创造雪花等语句
//计算下次的坐标等语句
call Snow( next_x[0], next_y[0], i - 1 )
call Snow( next_x[1], next_y[1], i - 1 )
call Snow( next_x[2], next_y[2], i - 1 )
call Snow( next_x[3], next_y[3], i - 1 )
//next_x 是 下一次的递归的X坐标数组
//next_y 是 下一次的递归的Y坐标数组
endfunction[/codes]
雪花函数最高耗费为:i(递归次数)* 雪花函数的耗费
但是这个最高耗费会出现:
4^i(4的i次方)次
这也是那贴上很多人测试后都觉得电脑扛不住的原因。
这个雪花函数是不能转换成迭代的(至少魔兽不行)。
但它可以不用递归:
办法:
首先,我们来深度探讨一下递归,我们递归,其实真正需要堆栈在里面放置的是递归函数的参数,利用参数不断的运算出下一次递归的参数,再将这个参数放进栈里,再运用这个参数进行运算…………………………直到递归结束。
而那些局部变量和返回的值的空间其实可以省略。
那么,既然堆栈是一个栈,那么我们能不能也创造一个栈,在其中只放下我们需要的参数,而其他的东西就通过一个函数来弄就好了。
在C++编程时,栈有两种:数组栈(顺序栈)和链式栈
由于Jass的限制,我们只能使用数组栈(顺序栈),而链式栈则是不可能实现的。
一个顺序栈,作为一个类,他会有:
1.存放元素的数组(可能会有多个)
2.top(栈顶的指针,其实它=有多少个元素-1)
3.maxSize(栈的最大存储量)
其中maxSize我们可以用魔兽中给定的:
[codes=jass] constant integer JASS_MAX_ARRAY_SIZE = 8192[/codes]
来进行比较(其实如果你递归的栈的数组中的元素超过了这个数,我建议你直接撞死,毕竟递归哪有调用自身最多8192次的………………&_&+囧)
实际办法是这样的:
若:雪花函数递归n次
则:用栈来记录上一次雪花函数的参数,然后顺序构造完最左边的一条边(在此过程中不断的将参数压入栈),直到构造完了所有的最左边的边(此时栈中元素为n-1个),然后使用此时栈顶的元素,依次构造完这次剩下的三条边(如果有其他的比雪花函数还复杂的结构,比如二叉树乃至N叉树,那么此时应继续按第二叉(=第二边)继续循环至第二条边的【极限】(还是以最左边为最优先),再循环至第三四条边的【极限】,此时,这次的循环达到【极限】,将这次的参数从栈中弹出,栈顶下移,使用此时栈顶的参数再进行剩下的边的循环………………直到第一次循环达到【极限】,将栈中最后一个元素弹出,【伪】递归结束),再将栈顶的元素弹出(栈顶随之下移),再利用此时栈顶的元素,构造第二条边,并构造这第二条边的4条边……………………直到所有的边全部构造完毕,雪花也就构造出来了。
花了1个小时,编出来了(哎………………)
[codes=jass]function GetSnowSideLeftX takes real xl, real yl, real xr, real yr, integer which_side returns real
local real v = 0.0
//v = 【获得雪花的边的左边的点的X坐标】
return v
endfunction
function GetSnowSideLeftY takes real xl, real yl, real xr, real yr, integer which_side returns real
local real v = 0.0
//v = 【获得雪花的边的左边的点的Y坐标】
return v
endfunction
function GetSnowSideRightX takes real xl, real yl, real xr, real yr, integer which_side returns real
local real v = 0.0
//v = 【获得雪花的边的右边的点的X坐标】
return v
endfunction
function GetSnowSideRightY takes real xl, real yl, real xr, real yr, integer which_side returns real
local real v = 0.0
//v = 【获得雪花的边的右边的点的Y坐标】
return v
endfunction
function CreateSnowSide takes real xl, real yl, real xr, real yr, integer which_side returns nothing
//创造指定的雪花(一条边上的)的边
endfunction
function Snow takes real x_l, real y_l, real x_r, real y_r, integer n returns nothing
local real array stack_xs_l //栈的左边的点X坐标的数组
local real array stack_ys_l //栈的左边的点Y坐标的数组
local real array stack_xs_r //栈的右边的点X坐标的数组
local real array stack_ys_r //栈的右边的点Y坐标的数组
local integer array stack_side //栈的边的数组/应处理哪个边
local integer stack_top = 0 //栈顶
local integer j = 0
local integer need = n - 1
if n >= JASS_MAX_ARRAY_SIZE then //是否大于maxSize?
call BJDebugMsg( "BS!程序没法弄这么多雪花的边,你和你的电脑去死吧!!!!" )
return
endif
set stack_xs_l[0] = x_l
set stack_ys_l[0] = y_l
set stack_xs_r[0] = x_r
set stack_ys_r[0] = y_r
set stack_side[0] = 0
//上面为初始化
loop
if stack_side[stack_top+1] != 4 then //如果下一层的边未处理完
set stack_xs_l[stack_top+1] = GetSnowSideLeftX( stack_xs_l[stack_top], stack_ys_l[stack_top], stack_xs_r[stack_top], stack_ys_r[stack_top], stack_side[stack_top] )
set stack_ys_l[stack_top+1] = GetSnowSideLeftY( stack_xs_l[stack_top], stack_ys_l[stack_top], stack_xs_r[stack_top], stack_ys_r[stack_top], stack_side[stack_top] )
set stack_xs_r[stack_top+1] = GetSnowSideRightX( stack_xs_l[stack_top], stack_ys_l[stack_top], stack_xs_r[stack_top], stack_ys_r[stack_top], stack_side[stack_top] )
set stack_ys_r[stack_top+1] = GetSnowSideRightY( stack_xs_l[stack_top], stack_ys_l[stack_top], stack_xs_r[stack_top], stack_ys_r[stack_top], stack_side[stack_top] )
//上面为计算坐标
set stack_top = stack_top + 1 //栈压入一层
else
set stack_side[stack_top+1] = 0 //初始化下层并列的另外的边的设定
set stack_side[stack_top] = stack_side[stack_top] + 1 //这层的要处理的边递增
set stack_top = stack_top - 1 //栈弹出一层
endif
if stack_top == need then //如果构造到要求的深度
loop
call CreateSnowSide( stack_xs_l[stack_top], stack_ys_l[stack_top], stack_xs_r[stack_top], stack_ys_r[stack_top], j )
set j = j + 1
exitwhen j > 3
endloop
//上面为创造四条边
set j = 0 //清空变量
set stack_side[stack_top] = stack_side[stack_top] + 1 //这层的要处理的边递增
if stack_side[stack_top] == 4 then //如果这一分支已达到极限
set stack_side[stack_top] = 0 //初始化这层并列的另外的边的设定
set stack_top = stack_top - 1 //栈弹出一层
set stack_side[stack_top] = stack_side[stack_top] + 1 //顺序处理下一个边
endif
set stack_top = stack_top - 1 //栈弹出一层
endif
exitwhen stack_top == -1 //如果栈中元素没有了(也就是所有的雪花都创造完成了),退出循环
endloop
endfunction[/codes]
PS:没有真正上机实验过,不能保证这上面的算法真的能用(但我觉得应该是没问题了)。
最后,说一句,大家在用Jass编程时基本很少遇到必须要递归解决的问题,所以大家最后不要故意使用递归,而且遇到使用递归的情况,都可以按我说的办,减少算法的耗费,要不然纯递归实在是太能“整”电脑了。
PS:…………………………实在不好意思再叫kook大人给我加精华了,可是我还是想加精华………………kook大人,能不能满足我一下呢? |
评分
-
查看全部评分
|